Tengo un nuevo reto para lo que queda de 2019 y para el primer semestre del 2020. He empezado a leer el libro Elementary Mechanics Using Python: A Modern Course Combining Analytical and Numerical Techniques, de Anders Malthe-Sørenssen. Es todo un curso de física, y combina de manera comprensible los ejemplos clásicos de movimiento, fuerzas, energía,… con sus soluciones numéricas, utilizando las libreriías matemáticas y de gráficos de Python.
Se trata de implementar todos los ejemplos del libro a código Python. No he visto ningún enlace para descargar todo el código, en cualquier caso, los ejemplos quiero adaptarlos y hacérmelos míos. He empezado por el ejemplo del peso suspendido de un muelle, que como todo el mundo sabe la solución del movimiento es sinusoidal entorno al punto de equilibrio, la velocidad es cero en los puntos máximo y mínimo, y la velocidad es máxima en el punto de equilibrio. Este ejemplo se explica en el apartado 5.7, que habla de fuerzas, y no basta con copiar y pegar el código, sino que lo he tenido que adaptar. Esta es mi solución:
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
# Initialize
m = 1.0
# kg
k = 100.0 # N/m
v0 = 1.0
# in m/s
time = 2.0 # s
g = 9.8 # m/s^2
# Numerical setup
dt = 0.0001 # s
n = int(round(time/dt))
t = np.zeros(n,float)
y = np.zeros(n,float)
v = np.zeros(n,float)
# Initial values
y[0] = 0.0
v[0] = v0
# Simulation loop
for i in range(n-1):
\tF = -k*y[i] – m*g
\ta = F/m
\tv[i+1] = v[i] + a*dt
\ty[i+1] = y[i] + v[i+1]*dt
\tt[i+1] = t[i] + dt
fig = plt.figure()
fig.suptitle(u»Objecte suspès d’una molla»)
plot1 = fig.add_subplot(211)
#plot1.set_xlabel(‘t [s]’)
plot1.set_ylabel(‘y [m]’)
plot1.xaxis.grid()
plot1.plot(t,y)
plot2 = fig.add_subplot(212)
plot2.set_xlabel(‘t [s]’)
plot2.set_ylabel(‘v [m/s]’)
#plot1.grid(axis=’y’)
#plt.grid(b=True, which=’minor’, color=’#666666′, linestyle=’-‘)
plot2.xaxis.grid()
plot2.plot(t,v)
for i in range(10, n-1, 400):
\tplot1.plot(t[i],y[i],’ob’)
\tplot2.plot(t[i],v[i],’ob’)
plt.show()
Estos son los capítulos y temas que se tratan en el libro:
4. Motion in One Dimension .
5. Forces in One Dimension .
6. Motion in Two and Three Dimensions
7. Forces in Two and Three Dimensions
8. Constrained Motion
9. Forces and Constrained Motion
10. Work
11. Energy
12. Momentum, Impulse, and Collisions
13. Multiparticle Systems
14. Rotational Motion
15. Rotation of Rigid Bodies
16. Dynamics of Rigid Bodies
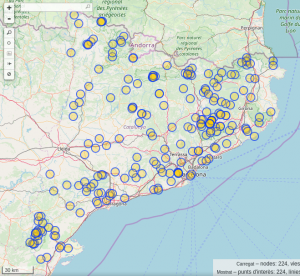
Ya tengo acabada la visualización de todos los dólmenes de Catalunya y Catalunya Nord. Se ha hecho este trabajo con varios propósitos. Por una parte, unificar y actualizar toda la información disponible en OpenStreetMap, donde sólo estaban listados la mitad de los dólmenes. También me interesaba la programación de OpenLayers para visualizar el mapa, y la renderización del mapa con diferentes estilos a parte del clásico de OSM.
